The chapter of number system is amongst the most important chapters in the whole of mathematics syllabus for virtually all the entrance exams inspite of the fact that is the most elementary concept in mathematics. The fundamentals of numbers would be applied across arithmetic in different forms in algebra and also as an extended feature in fundamental principal of counting.
NUMBER SYSTEM:
Number System presents the simplest mathematical structure. This system includes the real numbers, complex numbers, rational number, irrational numbers, fractions, integers, whole number and natural numbers.
Decimal Number System
The system of number we use in general is Decimal System. There are ten digits in this system 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. These are also the face value of the digits. The place value of a digit will change according to its position in unit’s place, ten’s place, hundred’s place and so on.
e.g.: In 2010, Face value of “2” is 2 and Place value of “2” is thousand.
Real Number
Set of all number that can be represented on the number line are called real numbers.
For example 6, -7, 0, 6.3777, 7, 7+, 3, 311, etc
A Number Line is a straight line with an arbitrary point called origin. To the right of this point are positive numbers and to the left are negative numbers.
Imaginary Numbers
In real number system square root of negative numbers does not exist. Solution of certain equations like x2 + 3 = 0 leads to the concepts of imaginary number. Numbers which are not equal. i is the imaginary unit whose value is √(-1) and it is written as i and known as iota.
Natural Numbers
N = {1, 2, 3, 4, 5, 6, ………….. } is the set of all natural numbers. These are counting numbers.
1 + 2 + 3 + 4 + 5 + _____________ + n = n (n+1)2
Can also have sum of first “n” odd and “n” even numbers together. One tends to remember all sum related formula together.
12 + 22 + 32 + 42 + 52 + ____________ + n2 = n(n + 1)(2n + 1)6
13 + 23 + 33 + 43 + 53 + ____________ + n3 = nn +122
Sum of first “n” odd numbers = n2, Sum of first “n” even numbers = n x (n+1)
Whole Numbers
W = {0, 1, 2, 3, 4, 5, 6, ………….} is the set of all whole numbers.
Whole numbers are natural numbers together with zero.
It is denoted as W = N + {0}
Integers
1 = {-3, -2, -1, 0, 1, 2, 3, ....} is the set of all integers. It is a set of all numbers, 0 and negative of natural numbers.
Positive Integers
These are all natural numbers, I + =- {1, 2, 3, 4, …………….}
Negative Integers
I = {-1, -2, -3, ---},
0 is neither positive nor negative.
Rational Numbers
The numbers of the form p/q where p & q are integers and q ≠ 0 are rational numbers, Every integer is a rational number.
Irrational Numbers
The numbers which when expressed in decimal form are in non-terminating and non repeating forms are called irrational number.
e.g. √3, √11, π, π is not 22/7. It is the approximate value of π
Even Numbers
These are denoted by the expression 2I where I is an integer.
2 + 4 + 6 + 8 + …………………. + 2n terms = n(n + 1) [Sum of even numbers = n(n + 1)]
Odd Numbers
These are denoted by the expression 2 I + 1 where I is an integer.
1 + 3 + 5 + 7 + 9 + …………………. + n terms = n2 [Sum of odd numbers = n2]
Prime Numbers
A number which has exactly two factors, 1 and the number itself, is called prime number.
e.g. 2, 3, 5, 7, 11,.....
The Pratham Edge: A Prime Number ≥ 3 is always expressed in the form 6k ± 1. However it is not a test to check whether its prime or not.
Composite Numbers
A number which has more than 2 factors is called a composite number.
e.g. 4, 6, 8, 9, 12, …………
Co-Primes
Two natural numbers a and b are said to be co-prime if their HCF is I.
Ex. (2, 3), (4, 5), (7, 9), (8, 11) etc. are pairs of co-primes.
TEST OF DIVISIBILITY
1. Divisibility By 2: A number is divisible by 2, if its unit’s digit is either 0, 2, 4, 6 or 8.
Ex. 84932 is divisible by 2, while 65935 is not.
2. Divisibility By 3: A number is divisible by 3, if the sum of its digits is divisible by 3.
Ex. 592482 is divisible by 3, since sum of its digits = (5 + 9 + 2 + 4 + 8 + 2) = 30, which is divisible by 3.
But, 864329 is not divisible by 3, since sum of its digits (8+6+4+3+2+9) = 32, which is not divisible by 3.
3. Divisibility By 4 : A number is divisible by 4, if the number formed by the last two digits of the number is divisible by 4.
Ex. 982648 is divisible by 4, since the number formed by the last two digits is 48, which is divisible by 4.
But, 749282 is not divisible by 4, since the number formed by the last two digits is 82, which is not divisible by 4.
4. Divisibility By 5 : A number is divisible by 5, if its unit’s digit is either 0 or 5. Thus, 20820 and 50345 are divisible by 5, while 30934 and 40946 are not.
5. Divisibility By 6 : A number is divisible by 6, if it is divisible by both 2 and 3.
Ex. The number 35356 is clearly divisible by 2.
Sum of its digits = (3 + 5 + 2 + 5 + 6) = 21, which is divisible by 3.
Thus, 35256 is divisible by 2 as well as 3. Hence, 35256 is divisible by 6.
6. Divisibility By 7: Subtract 2 times the last digit from the rest.
Ex: 483 is divisible by 7.
48-(3x2) = 42, which is divisible by 7.
7. Divisibility by 8 : A number is divisible by 8, if the number formed by the last three digits of the given number is divisible by 8.
Ex. 953360 is divisible by 8, since the number formed by last three digits is 360, which is divisible by 8.
But, 529418 is not divisible by 8, since the number formed by last three digits is 418, which is not divisible by 8.
8. Divisibility By 9 : A number is divisible by 9, if the sum of its digits is divisible by 9.
Ex. 60732 is divisible by 9, since sum of digits = (6 + 0 + 7 + 3 + 2) = 18, which is divisible by 9.
But 68956 is not divisible by 9, since sum of digits (6 + 8 + 9 + 5 + 6) = 34, which is not divisible by 9.
9. Divisibility By 10 : A number is divisible by 10, if it ends with 0.
Ex. 96410. 10480 are divisible by 10, while 96375 is not.
10. Divisibility By 11 : A number is divisible by 11, if the difference of the sum of its digits at odd places and the sum of its digits at even places, is either 0 or a number divisible by 11.
Ex. The number 3832718 is divisible by 11, since :
(sum of digits at odd places) - (sum of digits at even places)
= (8 + 7 + 3 + 3) - (1 + 2 + 8) = 11, which is divisible by 11.
11. Divisibility By 12 : A number is divisible by 12 if it is divisible by both 3 and 4.
12. Divisibility by 14 : Add the last two digits to twice the rest. The answer muss be divisible by 14
Ex : 364 = (3 x 2) + 64 = 70 is divisible by 7
13. Divisibility By 15: A number is divisible by 15 if it is divisible by both 3 and 5.
14. Divisibility By 16: A number is divisible by 16 if the number formed by its last four digits is divisible by 16.
15. Divisibility By 17: Subtract 5-times the last digit from the rest.
Ex: 221 = 22- (1 x 5) = 17 is divisible by 17
16. Divisibility By 19: Add twice the last digit to the rest.
Ex: 437 = 43 + (7 x 2) = 57 is divisible by 19
17. Divisibility By 20: If the number formed by the last two digits is divisible by 20.
Ex: 480 = (80 is divisible by 20). So, the number is divisible by 20.
18. Divisibility By 25 : A number is divisible by 25 if the number formed by its last two digits are either 25, 50, 75 or 00. and so on...
Note : If a number is divisible by p as well as q, where p and q are co-primes, then the given number is divisible by pq. If p and q are not co-primes, then the given number need not be divisible by pq, even when it is divisible by both p and q.
Example. 36 is divisible by both 4 and 6, but it is not divisible by (4 x 6) = 24, since they are not co-prime.
DIVISION ALGLORITHM
If we divide a given number by another number, then:
Dividend = (Divisor x Quotient) + Remainder
(i) (xn – an) is divisible by (x - a) for all values of n.
(ii) (xn – an) is divisible by (x + a) for all even values of n.
SIMPLIFICATIONS
1. ‘BODMAS’ Rule: This rule depicts the correct sequence in which the operations are to be executed, so as to find out the value of a given expression.
Here, ‘B’ stands for ‘Bracket sequencially (), {}, [], ‘O’ for ‘of’, ‘D’ for ‘Division’, ‘M’ for ‘Multiplication’, ‘A’ for ‘Addition’ and ‘S’ for ‘Subtraction’.
Thus, in simplifying an expression, first of all the brackets must be removed, strictly in the order ( ), { } and [ ]. After removing the brackets, we must use the following operations strictly in the order:
(i) of (ii) Division (iii) Multiplication (iv) Addition (v) Subtraction.
2. Simplification : When an expression contains Virnaculum, before applying the ‘BODMAS’ rule, we simplify the expression under the Virnaculum.
BASIC FORMULAE
1. (a + b)2 = a2 + b2 + 2ab
2. (a - b)2 = a2 + b2 - 2ab
3. (a + b)2 - (a - b)2 = 4ab (Avoid in basic formula...It can be-easily derived & one doesn’t need to remember it)
4. (a + b)2 + (a - b)2 = 2 (a2 + b2)
5. (a2 - b2) = (a + b) (a - b)
6. (a + b + c)2 = a2 + b2 +c2 + 2(ab + bc + ca)
7. (a3 + b3) = (a + b) (a2 - ab + b2)
8. (a3 - b3) = (a - b) (a2 + ab + b2)
9. (a3 + b3 + c3 - 3abc) = (a + b + c) (a2 + b2 + c2 - ab - bc - ac)
10. If a + b + c = 0, then a3 + b3 + c3.
11. (a4 - b4) = (a + b) (a – b)(a2 + b2)
12. (a + b)3 = a3 + b3 + 3ab (a + b)
13. (a - b)3 = a3 - b3 - 3ab (a - b)
Recurring Decimal = If in a decimal fraction, a figure or a set of figures is repeated continuously, then such a number is called a Recurring Decimal.
eg. 0.878787 = 0.87
Vulgar Fraction = A fraction in which the denominator is not 10 or powers of 10.
To Convert a Pure Recurring Decimal into Vulgar Fraction:
Rule: Write the repeated figure or figure only once in the numerator without decimal point and take as many 9’s in the denominator as is the number of repeating figures.
Example 1: Express the following as vulgar fraction:
(i) 0.7 (ii) 0.14 (iii) 0.057
Solution: Using the above law, we have:
(i) 0.7 = 7/9 (ii) 0.14 = 14/99 & (iii) 0.057 -= 57/999
To convert a Mixed Recurring Decimal to Vulgar Fraction:
Rule: In the numerator take the difference between the number formed by all the digits after decimal point (taking repeated digits only once) and that formed by the digits which are not repeated. In the denominator, take the number formed by as many nines as there are repeating digits followed by as. many zeros as is the number of non-repeating digits.
Example 2 Express the following as vulgar fractions:
(i) 0.17 (ii) 0.1254 (iii) 2.634
Solution: Using the above rule, we have :
(i) 0.17 = 17-190=1690=845
(ii) 0.1254 = 1254-129900=12429900=69550
(iii) 2.634 = 2 + 634-63900=2+571900=2371900
Indices and Surds
1. ap x aq x ar = a(p + q + r)
2. (ap)q = apq
3. a0 = 1
4. a-p = 1/ap
5. 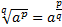
6. (ab)p = ap x bp
7. 
8. a(p)q = (ap)q for example (23)3 = 29 = 512 and (23)2 = 26 = 64
Logarithm
N = ax, Then IogaN = X
So logarithm of a number to a particular base is the power to which the base must be raised to get the number: Logarithm of a negative number is not defined.
1. loga(XY/Z) = logaX + logaY - logaZ
2. logaZk = k logaz
3. logxx = 1
4. log101 = 0, log 1010= 1
6. If logaxy = logax + logay
loga(x/y) = logax - logay
7. logbn am =  (m/n) logb a
(m/n) logb a
HCF and LCM
Least Common Multiple (LCM) of two or more numbers is the least number which is divisible by each of these numbers (i.e. leaves no remainder; or remainder is zero). The same can be algebraically defined as “LCM of two or more expressions is the expression of the lowest dimension which is divisible by each of them i.e. leaves no remainder; or remainder is zero.”
Highest Common Factor (HCF) is the largest, factor, of two or more given numbers. The same can be defined algebraically as “HCF of two or more algebraically expressions is the expression of highest dimension which divides each of them without remainder.
HCF is also GCD (Greatest Common Divisor)
Product of two numbers (a x b) LCM x HCF
LCM is a multiple of HCF
For product of three numbers (a, b, c)
LCM =
For product of four numbers (a, b, c, d)
LCM =
For finding LCM and HCF of fractions, first reduce each fraction to its simplest form i.e., cancel out any common factors between the denominator and numerator and then apply appropriate formula from the following
HCF of fractions = (HCF of numerators)/(LCM of denominators)
LCM of fractions = (LCM of numerators)/ (HCM of denominators)
The power of HCF in the denominator remains one less than the number of numbers.
In word problems involving “longest”, “highest”, “tallest”, “largest”, “maximum” etc. we find HCF in word problems involving “shortest”, “smallest”, “least”, “minimum” etc. we find LCM.
Other Quants Notes:







