Simple Interest & Compound Interest
A clear understanding of percentage calculations is a prerequisite to solve the problems in interest. The solved example of this chapter will help you in different dimensions, This chapter finds its varied application in solving data interpretation problems.When a sum of money is lent by x to y, then x is called the lender or creditor and y is called the debtor or borrower. The money borrowed is called Principal or Sum.Extra money paid for using other’s money is called Interest.Total money paid in the end is the sum of Principal & Interest and is known as Amount.Growth of money can be simple or compound.
IMPORTANT POINTS ON INTEREST
Simple Interest:
If the interest on certain sum for a certain period is reckoned uniformly, it is called Simple Interest (SI)
At simple rate the simple interest is proportional to the time.
There is no interest on interest.
The interest is calculated on the initial sum.
The amounts are in AP if time is same.
Formulae.
Let Principal = P, Rate = R% and time = T years. Then
S.I. = 
P = 
T = 
R = 
Compound Interest:
Interest which is calculated on the initial principal well as the interest accumulated over previous periods is called Compound interest (C.I.)The amount at the end of certain year becomes the principal for the next time period.At Compound rate there is interest on interest.The ratio between the amounts at compound rate is same if the time is same.
The amounts at compound rate are in G.P. if time is same.
FORMULAE :
Let Principal = P, Rate = R% and Time = n years. Then
1.When interest is compounded Annually:
In this case, Amount = 
2.When interest is compounded Half Yearly:
In this case, Amount = 
3. When interest is compounded Quarterly:
In this case, Amount = 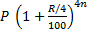
4. When Time is Fraction of a Year:
Let the time be a fraction of a year, say 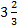 years
years
Then Amount = 
5. When interest is compounded continuously, Amount = P{e(rt/100)}
6. When Rates are different for different years, say R1, R2, R3, percent for 1st, 2nd and 3rd year respectively:
In this case, Amount = 
Under Compound Interest, the interest is added to the principal at the end of each period to arrive at the new principal for the next period.In other words, the amount at the end of first year (or period) will become the principal for the second year (or period); the amount at the end of second year (or period) becomes the principal for the third year (or period) and so on.
If P denotes the principal at the beginning of Period 1, then principal at the beginning of Period 2
= 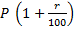
= PR = Amount at the end of Period 1 P at the beginning of Period 2
= 
= PR2 = Amount the end of Period 2 P at the beginning of Period (n + 1)
=  = PR2
= PR2
= Amount at the end of period n
Where R = 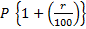
Hence the amount after n years (periods) = PRn = A
Interest = I = A - P = P [Rn - 1]
Example 1.Calculate the simple interest on Rs7200 for 4 years at 6.25% p.a. rate.
Solution : Simple Interest = 25% of 7200 = Rs. 1800
Example 2 Rate is 10% p.a., Time is 4 years, What is the simple Interest on a loan of Rs. 1000.
Solution: Simple Interest = 40% of Rs. 1000 = Rs 400
Example 3 A sum becomes 2.6 times in 8 years at simple rate. Find the rate.
Solution:The Rate is  x 100 = 20%, because the rate is the interest on Rs. 100 in one year.
x 100 = 20%, because the rate is the interest on Rs. 100 in one year.
Example 4. A sum becomes 3 times in 8 years at simple rate. When does it become 5 times?
Solution: Let the P = Rs. 1
S 1 is Rs. 2 in 8 years
S 1 is Rs. 4 in 16 years [When SI = Rs. 4, A = Rs. 5 hence 5 times]
Ans = 16 years
Example 5. What sum amounts to Rs 6400 in 4 years at 3.75% p.a. simple rate.
Solution: Amount after 4 years = (100 + 4 x 3.75)% of Principal
6400 =  x Principal
x Principal
Principal = Rs 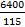 x 100 = Rs. 5565.25
x 100 = Rs. 5565.25
Alternate Method: Use direct formulae P = (100 x A)/(100 + RT)
Example 6. A sum becomes Rs. 1200 after 2 years & Rs. 1320 after 3 years at simple rate. Find the rate.
Solution: P = 1200, t = 1 year
SI = A - P 1320 - 1200 = 120
Rate = (100 x 120)/(1200) = 10%
Example 7.Simple interest of 2 years = Rs. 600. Find the compound interest on the same sum at 20% p.a. rate.
Solution:C.I. of 2 year = Rs. 600 + 20% of Rs. 300 [Rs. 300 is S.I. in 1 year]
Rs 660
Example 8 .What sum amounts to Rs. 9261 in 3 years at 5% p.a. compound interest.
Solution: = 9261
= 9261
P = Rs. 8000
Example 9 .A sum becomes  times in 2 years at compound rate. Find the rate.
times in 2 years at compound rate. Find the rate.
Solution:Since the sum becomes 25/4 times after 2 years.
If becomes  = 5/4 after 1 year
= 5/4 after 1 year
Rate =  = 25%
= 25%
Example 10.For how many years should Rs. 600 be invested at 10% per annum in order to earn the same simple interest as earned by investing Rs. 800 at 12% per annum for 5 years?
Solution:Simple Interest = Rs.  = Rs. 480
= Rs. 480
Time =  = 8 years
= 8 years
Other Quants Notes:







