Time Speed and Distance
Your ability to solve the problems on relative motion, circular motion, and problems
based on trains, boats, clock, races etc. will depend only on the depth of your
understanding
1. Speed Distance/Time
2. Distance = Speed x Time
3. Time = Distance/ Speed
4. x km/hr = (x x 5/18) m/sec
5. y m/sec = (y x 18/5) km/hr
6. If a certain distance is covered at x km/hr and the same distance is covered at
y km/hr, then the average speed during the whole journey = 
km/hr
km/hr
7. If a person changes his speed in the ratio m: n. then the ratio of time taken
becomes n : m
8. For the same distance speed varies inversely as time and in the same time
distance varies directly as speed
9. Average Speed = 
Please note that the average speed of a moving body is NOT EQUAL to the average
of the speed
10. If a body covered one part of the journey at speed p and the remaining part of
the journey at speed q and the distances of the two parts of the journey are in the
ratio m : n, then the average speed for the entire journey is
Conversions
-
To convert cm to metre divide by 100.
-
To convert km to min. multiply by 1000.
-
To convert hours to min. multiply by 60.
-
To convert hours to sec multiply by 3600.
-
To convert minutes to hours divide by 60.
- To convert seconds to hours divide by 3600.
Example 1.Time taken at 48 km/h is 24 minutes. What is the time if speed
decreases by 25%?
Solution:Speed ratio = 4: 3
Time ratio 3: 4 = 24: 32
Time ratio = 32 minutes
Example 2. Walking at 48% less speed, time taken is 75 minutes. Find the time
taken a usual speed.
Solution:Speed ratio = 100 : 52 25 : 13
Time ratio = 13 : 25 (speed and time vary inversely)
= 39 : 75
Time = 39 minutes
Example 3.A 240m long train travelling at 36 km/h clears a 600 m long platform in
how much time.
Solution: Speed of Train = 36 x 5/18 m/s 10m/sec.
Time = Distance/Speed 840m/10m/s = 84sec.
Example 4. A train at 148 km/h .overtakes a motorcyclist at 58 km/h in the same direction in 10 sec. What is the length of the train?
Solution:Distance = Speed x time
= (148 - 58) x 5/18 x 10m 250m
Example 5.Speed from A to B = 10 km/h and from B to A is 40 km/h. What is the average speed?
Solution:Average Speed = 2 x 10 x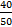 
= 16 km/hr.
= 16 km/hr.
(If the distance is same then average speed is the harmonic mean)
Trains
Relative Speed:
The speed of one (moving) body in relation to another moving body is called the
relative speed of these two bodies, i.e., it the speed of one moving body as
observed, from the second moving body.
If two bodies are moving in the same direction, the relative speed is equal to the
difference of the speed of the two bodies.
If two bodies are moving in the opposite direction, the relative speed is equal to the
sum of the speeds of the two bodies.
-
When a train crosses a tree/pole etc. Time taken to cross in seconds x speed in m/s = length of the train in m.
-
When a train crosses a platform/tunnel/bridge etc. Time taken to cross in seconds x speed in m/s = length of the train in m + length of platform/tunnel/bridges in m.
-
In problems on two trains the lengths of the trains are always added irrespective of whether the trains are running in same or opposite directions on parallel tracks.
- If trains are running in opposite directions.
Time taken to completely cross each other = 
- If trains are running in same directions
Time taken by faster train to completely overtake the slower train
= 
- If two objects pass each other while travelling in the same direction then the
time taken to pass = 
Example 1.What is the time taken by a train running at 72 km/hr to cross a man
standing on a platform, the length of the train being 180 m?
Solution: Speed of train = 72 kmph = 72 x 
= 20 m/s
= 20 m/s
Distance = length of the train = 180 m
Time = 
= 9 sec
= 9 sec
Example 2. How long will a train 100m long and traveling at a speed of 45 kmph,
take to cross a platform of length 250 m?
Solution: Distance = length of the train + length of the platform = 100 + 250 = 350m
Speed of the train = 45 kmph
= 45 x 
= 12.5 m/sec.
= 12.5 m/sec.
Therefore, Time = 
= 28 sec.
= 28 sec.
Example 3. Find the length of bridge, which a train 120 m long traveling at 54 kmph
can cross in 30 seconds.
Solution: Speed of the train = 54 kmph = 54 x 
= 15 m/sec
= 15 m/sec
Distance covered in 30 seconds = 15 x 30 = 450 m
Length of bridge = Distance covered — Length of the train = 450 - 120 = 330 m.
Boat and Stream
Problems related to boats and streams are different in the computation of relative
speed from those of train/cars.
When a boat is moving in the same direction as the stream or water current, the
boat is said to be moving
WITH THE STREAM OR CURRENT.
When a boat is moving in a direction opposite to that of the stream or water current,
it is said to be moving
AGAINST THE STREAM OR CURRENT.
If the boat is moving with a certain speed in water that is not moving, the speed of
the boat is then be called the
SPEED OF THE BOAT IN STILL WATER.
When the boat is moving upstream, the speed of the water opposes (and hence
reduces) the speed of the boat.
When the boat is moving downstream, the speed of the water add (and thus adds to)
the speed of the boat.
Thus have
Speed of the boat against stream = Speed of the boat in still water - Speed of
the stream
Speed of the boat with the stream = Speed of the boat in still water + Speed of
the stream
Relative Speed
If u is the speed of the boat down the stream and v is the speed of the boat up the
stream, then we have the following two relationships,
-
Speed of the boat in still water =
-
Speed of the water current =
Following relations shall also be useful
-
Speed of boat in still water =
[speed downstream + speed upstream]
-
Speed of stream =
[speed downstream - speed upstream]
-
If speed of boat in still water is b km/hr, speed of river or stream is s km/hr, speed downstream is d km/hr and speed upstream is u km/hr then
d = (b + s) km/hr and u = (b - s) km/hr
b = 
(u + d) km/hr and s = 
(u - d) km/hr
(u + d) km/hr and s = (u - d) km/hr
NOTE : In problems, instead of a boat, it may be a swimmer but the approach is
exactly the same, instead of boats/swimmers in water. It could also be a cyclist
cycling against or along the wind. The approach to solve problems still remains the
same.
Example 1. A boat travels 30km upstream in 6 hours and 20 km downstream in 5
hours. Find the speed of the boat in still water and the speed of water current.
Solution: Upstream speed = 30/6= 5 kmph
Downstream speed = 20/5 = 4 kmph
Speed in still water = (5 + 4)/2 = 4.5 kmph
Speed of the water current = (5 - 4)/2 = 0.5 kmph
Example 2. A man can row 8 km in one hour in still water. If the speed of the water
current is 2 km/hr and it takes 3 hours for him to go to a new place and return, find
distance from the starting point to the new place.
Solution: Let the distance be x km
Upstream speed = 8 - 2 = 6 kmph
Downstream speed = 8 + 2 = 10 kmph
Total time = time taken upstream + time taken down stream = 
kmph
kmph
x = 11.25 kmRACES & TRACKS
When two persons P and Q are running a race, they can start the race at the same
time or one of them may start a little later than the other. In the second case
suppose P starts the race and after 5 seconds, Q starts. Then we say P has a “start”
of 5 seconds. Alternatively, in a race between P and Q. P starts first and then when
P has covered a distance of 10 meters, Q starts. Then we say that P has a “start” of
10 meters.
In a race between P and Q where Q is the winner, by the time Q reaches the winning
post first. If P still has another 15 meters to reach the winning post, then we say that
Q has won the race by 15 meters. Similarly, if P reaches the winning post 10
seconds after Q reaches it, then we say that Q has won the race by 10 seconds.
In problems on RACES, we normally consider a 100 m race or a 1 km race. The
length of the track NEED NOT necessarily be one of the two figures mentioned
above but can be as given in the problem.
When two or more persons running around a circular track (starting at the same
point and at the same time), then we will be interested in two main issues:
-
When they will meet for the first time and
-
When they will meet for the first time at the starting point
To solve the problems on circular tracks, you should keep the following points in
mind.
When two persons are running around a circular track in OPPOSITE directions
-
The relative speed equal to the sum of the speeds of the two individuals and
-
From one meeting point to the next meeting point, the two of them TOGETHER cover a relative distance equal to the length of the track.
When two persons are running a circular track in the SAME direction.
-
The relative speed is equal to the difference of the speeds of the two individuals and
-
From one meeting point to the next meeting point, the faster person covers one COMPLETE ROUND more than the slower person.
Please note that when we have to find out the time taken by the persons to meet for
the first time at the starting point, what we have to do is to find out the time taken by
each of them to complete one full round and then take the LCM of these two timings
(L/a and L/b are the timings taken by the two of them respectively to complete on
full round).
When three people are running around a circular track
Let the three people A, B and C with respective speeds of a, b and c (a > b > c) be
running around a circular track (of length L) starting at the same point at the same
time In this case we consider the three persons running in the same direction as the
general case.
Example 1: In a race of 1000 m. A beats B by 50 m or 5 seconds.
Find (i) B’s speed (ii) A’s speed (iii) Time taken by A to complete the race.
Solution: Since A beats B by 50 m, it means by the time A reaches the winning
point, B is 50 m away and as A beats B by 5 seconds, it means B takes 5 seconds to
reach the winning point. This means B covers 50 m in 5 seconds i.e., B’s speed is
50/5 = 10 m/s. Since A wins by 50 m, in the times A covers 1000 m, B covers 950 m
at 10 m/s, B can cover 950 m in 950/10.
i.e., 95 seconds i.e., 1 min 35 seconds.
A completes the race in 1 min 35 seconds
A’s speed is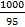 
= 
m/s
= m/s
Example 2. Rakesh runs 
times as fast as Mukesh. In a race, if Rakesh gives a
times as fast as Mukesh. In a race, if Rakesh gives a
lead of 60 m to Mukesh. Find the distance from the starting point where both of
them will meet.
Solution: Since Rakesh runs 
times as fast as Mukesh, in the time Mukesh runs
times as fast as Mukesh, in the time Mukesh runs
3 meters, for every 4 meters he runs.
Since he has given a lead of 60m, he will gain this distance by covering 4 x 60 =
240m
Hence they will meet at a point 240 m from the starting point
Example 21 In a 1500 m race, Tarun beats Manoj by 150 m and in the same race
Manoj beats Rahul by 75 m. By what distance does Tarun beat Rahul
Solution: Let us write the data given as below
This will be equal to 1350 x 
= 1282.5
= 1282.5
But Manoj running 1350 m is the same as Tarun running 1500m. Hence, Tarun beats
Rahul by m.
Other Quants Notes:
